反応器計算におけるQ学習2
はじめに
以前の記事で管型反応器において所望の反応率を得るという問題について強化学習(Q学習)を適用したが、 今回は反応率に応じて目的成分の選択率が変化するという条件で、収率を最大化する問題を対象とする。
管型反応器の例題
対象とする問題は下記の通り。
- 成分Aを反応して目的の生成物Bを得る管型反応器がある
- 反応器は連続運転しており、1日に1回だけAの反応率とBの収率を確認でき、その際に反応温度を変更することができる
- 反応温度は1回につき0.5℃変更できる(上げることも、下げることも、変えないことも可能)
- 反応温度を変更することで反応率を変化させることができる
- 生成物Bと一緒に副生物Cも生成し、反応率に応じて生成物Bの選択率は変化する
ある初期温度で運転を開始したのちに、収率を最大化することを学習できるか?
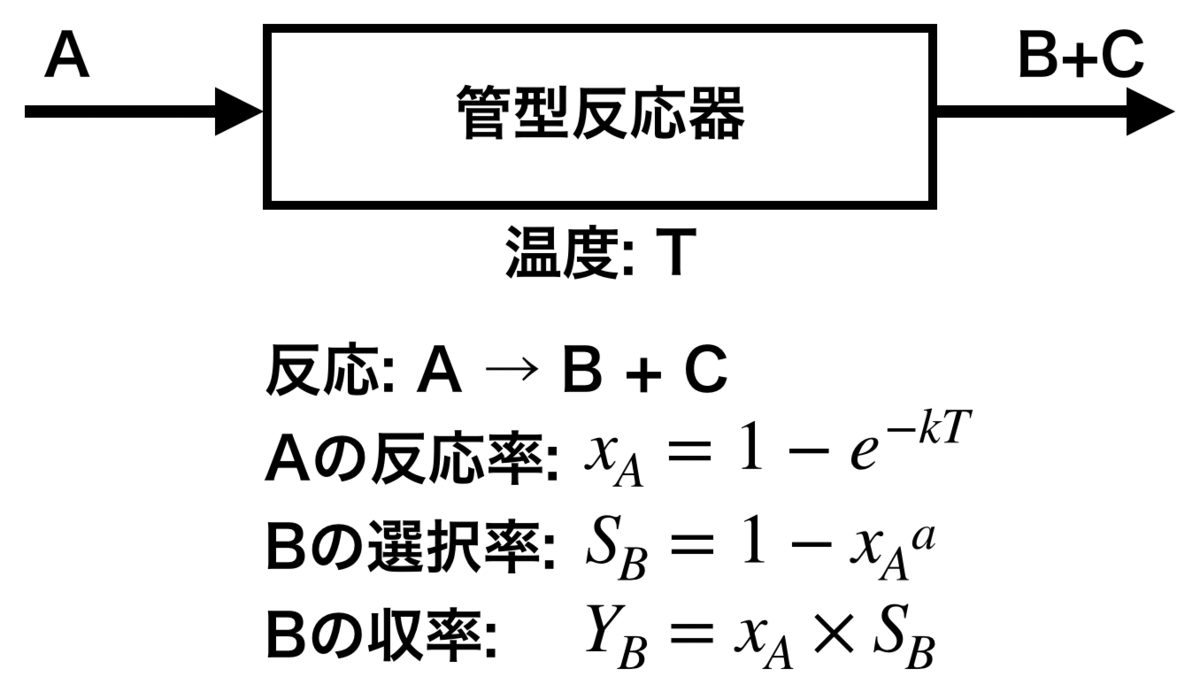
ここで反応温度・反応率・選択率・収率の関係は図中の式で表されるものとし、 本例題ではk=0.01、a=100とする。 反応温度と反応率、反応率と選択率の関係は下記グラフとなる。
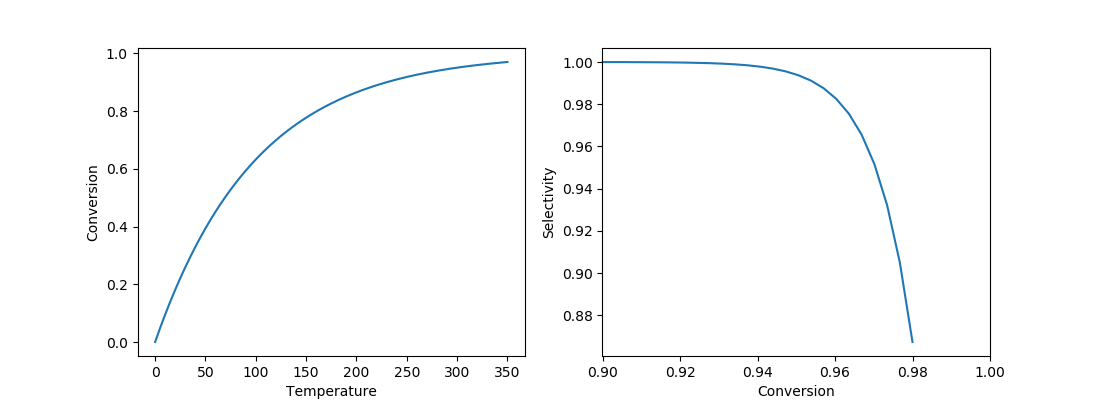
なお、収率が最大となる条件はこの時点で計算可能であり、反応率0.955、収率0.945である。 これを強化学習で推算できるかがポイントとなる。
管型反応器のモデル
反応器の状態と行動を次の表の通り整理する。 状態は反応率を離散化して表現する。ここでは反応率0.9未満を状態0とし、0.9から1.0を100分割して番号を振った。 (収率が最大となる反応率が少なくとも0.9以上とわかっている前提)
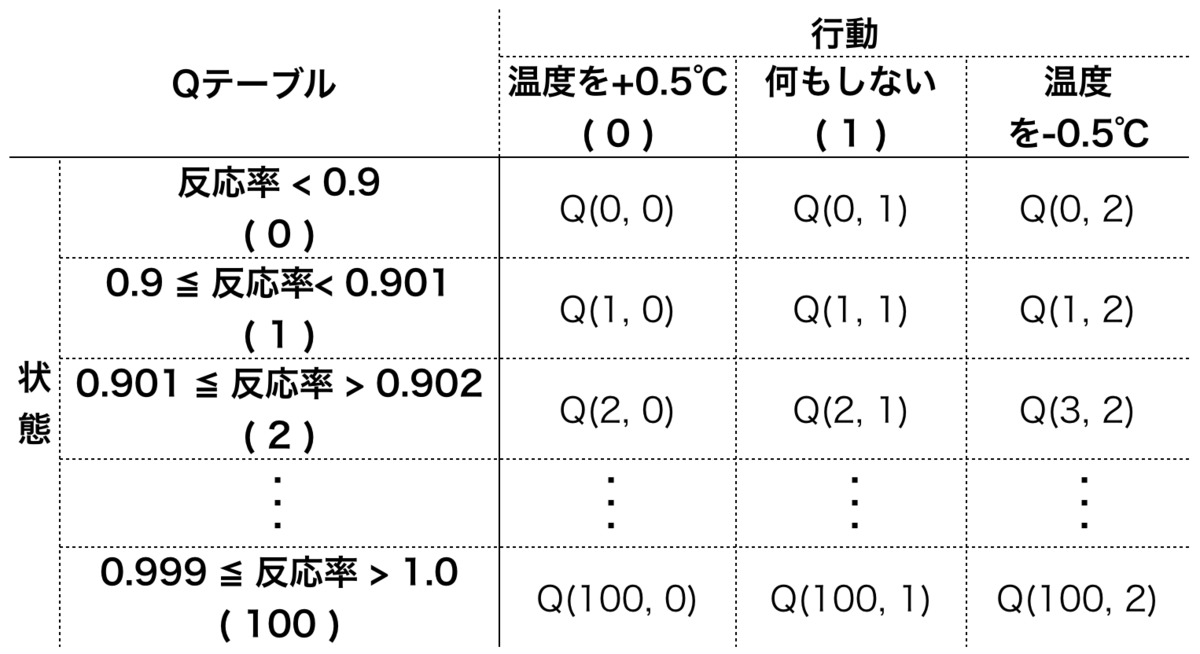
報酬はとし、1に満たない分をマイナスの報酬(ペナルティ)として与える形とした。
import numpy as np import matplotlib.pyplot as plt class Tubular_selec(object): def __init__(self, temp): self._k = 0.01 # kを0.01とする self._a = 100.0 # aを100とする init_conv = self.calc_conv(self._k, temp) init_yield = self.calc_yield(self._a, init_conv) ## ログとして[温度, 反応率, 収率]を残す self._log = [[temp, init_conv, init_yield]] def calc_conv(self, k, temp): ## 反応率計算 return 1 - np.exp(-k * temp) def calc_selc(self, a, conv): ## 選択率計算 return 1 - conv**a def calc_yield(self, a, conv): ## 収率計算 return conv * self.calc_selc(a, conv) def state(self): ## 状態を返す 状態を転化率0.9-1.0の間で100分割する ## 0.9未満を状態0とするので、状態は全部で101個 _, conv, _ = self._log[-1] # 一番最新のlogからデータ取得 n = 100 if conv < 0.9: # 反応率 0.1未満は状態0とする st = 0 else: st = int(np.ceil((conv - 0.9)*10*n)) # 0.9~1.0をn分割 return st def step(self, action): temp, _, _ = self._log[-1] # 最新の温度を取得 ## 行動0で温度UP、行動2で温度Down、行動1は何もしない if action == 0: temp += 0.5 elif action == 2: temp -= 0.5 conv = self.calc_conv(self._k, temp) yild = self.calc_yield(self._a, conv) self._log.append([temp, conv, yild]) # 1.0に満たない分を負の報酬(ペナルティ)として与える reward = - abs(1.0 - yild) return reward
Q値に従った次の行動の決定
def decide_action(qtable, state, episode): eps = 1 - episode/240 # ε-グリーディー法 if eps <= np.random.uniform(0, 1): # グリーディー行動 t = np.where(qtable[state]==qtable[state].max())[0] # Q値が最大のインデックスを返す else: # ランダム行動 t = np.arange(qtable.shape[-1]) # 取りうる行動すべて return np.random.choice(t) # 行動の候補からランダムに選ぶ
Q値の更新
def update_qtable(qtable, state, action, reward, next_state): gamma = 0.9 alpha = 0.5 next_qmax = max(qtable[next_state]) qtable[state, action] = (1 - alpha) * qtable[state, action] + alpha * ( reward + gamma * next_qmax) return qtable
学習する
1episodeあたり100日運転することとして、300episode学習させる。
OPERATION_PERIOD = 100 # 100日分 EPISODE_NUM = 300 qtable = np.zeros((101, 3)) # サイズは状態数✕行動数 ## 学習状況確認用グラフ設定 fig = plt.figure(figsize=(11,4)) ax1 = fig.add_subplot(121) ax2 = fig.add_subplot(122) ## 学習 for episode in range(EPISODE_NUM): #t = np.random.uniform(280, 350) # 初期温度をランダムにする場合 env = Tubular_selec(280) for d in range(OPERATION_PERIOD): ## まず現在の状態を確認 state = env.state() ## 次に行動を決める action = decide_action(qtable, state, episode) ## 決めた行動に従い運転を1日進める.また報酬を環境から得る reward = env.step(action) ## 新しい状態を確認 next_state = env.state() ## Qテーブル更新 qtable = update_qtable(qtable, state, action, reward, next_state) ## 10episodeにつき1回のグラフ描画 if (episode+1)%10 == 0: t, c, y = np.array(env._log).T ax1.cla() ax2.cla() ax1.set_xlabel("Days") ax1.set_ylabel("Temperature") ax1.set_ylim(270,320) ax2.set_xlabel("Days") ax2.set_ylabel("Conversion, Yield") ax2.set_ylim(0.93,0.96) ax1.plot(t) ax2.plot(c, label="Conversion") ax2.plot(y, label="Yield") ax2.legend() plt.pause(0.1)
学習結果
収率最大となるのは反応率0.955、収率0.945のときであるが、 反応温度を上げて、まっすぐその状態に近づいていることが確認できる。
