メモ: Python defaultdict の使い方
辞書型は存在しないキーを参照しようとするとエラーになるが、
>>> d = {}
>>> d['a']
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: 'a'
defaultdictは存在しないキーを参照すると、自動的にそのキーのデータを生成する
>>> import collections >>> dd = collections.defaultdict(int) >>> dd['a'] 0 >>> dd defaultdict(<class 'int'>, {'a': 0})
自動的に生成されるデータ値はdefaultdict()の()内の関数で初期化される。上の場合はint()が実行される(int()はint型の0が返る)。例えば次のようにすると'ああああ'で初期化される。
>>> func = lambda: 'ああああ' >>> dd = collections.defaultdict(func) >>> dd[0] 'ああああ' >>> dd['い'] 'ああああ' >>> dd defaultdict(<function <lambda> at 0x7fbb199c5dc0>, {0: 'ああああ', 'い': 'ああああ'})辞書型に次々に新しいキーのデータを追加する必要がある場合に便利と思われる。
OpenAI Gym 基本的な使い方のメモ
はじめに
すぐに使い方を忘れてネットで調べているので、基本的な使い方をメモしておく。ObservationWrapperの使用例も記載する。
基本的な使い方
CartPole
環境の構築(環境インスタンス生成)
import gym env = gym.make("CartPole-v0")
環境の初期化。観測値が返る
env.reset() >>> array([ 0.01308375, -0.00076966, 0.03593438, -0.04269914])
actionの数の確認
env.action_space >>> Discrete(2) # Discrete型 env.action_space.n >>> 2 # 数値で取り出せる
actionをランダムサンプリング
env.action_space.sample()
>>> 0
observation_spaceの型、上下限値、(次元)、数値型
env.observation_space >>> Box(-3.4028234663852886e+38, 3.4028234663852886e+38, (4,), float32)
observation_spaceの次元の数を数値で得る
env.observation_space.shape[0] >>> 4
observation をランダムサンプリング
env.observation_space.sample() >>> array([ 3.4541728e+00, -2.6457083e+38, -2.0181824e-01, -5.4519964e+37], dtype=float32)
環境に対しactionし、その後の観測値、報酬、終了判定フラグ、追加情報 を得る
action = 0 env.step(action) >>> (array([ 0.01306835, -0.19638798, 0.0350804 , 0.26110135]), 1.0, False, {})
FrozenLake
環境の構築と初期化
env = gym.make("FrozenLake-v0") env.reset() >>> 0 # 観測値は数値1つ
action_space と observation_space
env.action_space >>> Discrete(4) env.observation_space >>> Discrete(16) # 観測値はDiscrete型
ObservationWrapper
FrozenLakeのobservation_spaceはDiscrete型で0 - 15の数値が1つ返るが、これをOne-hotにエンコーディングしたいときにObservationWrapperを利用すると便利である。
observation_spaceをOne-hotなBox型に変えるWrapper
import gym.spaces import numpy as np class OneHotWrapper(gym.ObservationWrapper): def __init__(self, env): super(OneHotWrapper, self).__init__(env) shape = (env.observation_space.n,) self.observation_space = gym.spaces.Box(0.0, 1.0, shape, dtype=np.float32) def observation(self, observation): res = np.copy(self.observation_space.low) # 観測データの最小値を取る、つまり 0 res[observation] = 1.0 return res
環境の構築と初期化、および環境へのaction実施。観測値がOne-hotになっている
env_oh = OneHotWrapper(gym.make("FrozenLake-v0")) env_oh.reset() >>> array([1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32) action = 1 env_oh.step(action) >>> (array([0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32), 0.0, False, {'prob': 0.3333333333333333})
メモ: Miniconda インストール on macOS
はじめに
Anacondaは便利だが使うことのないパッケージがかなり大量に入っていて、ストレージに余裕のない状況ではつらいのでMinicondaを入れてみる。
準備
こちらに公式のinstructionがあるので一読しておく。
Installation — conda 4.9.2.post24+e37cf84a documentation
インストール
Macについてはこちらに手順が記載されている。
Installing on macOS — conda 4.9.2.post24+e37cf84a documentation
インストーラをインストールしたいフォルダに置き、ターミナルで下記を実行する。
bash Miniconda3-latest-MacOSX-x86_64.sh
途中でライセンスの同意と初期設定の実施要否を聞かれるのでyes を回答する。これでMinicondaへのPATHが通される(.bash_profile にPATHの内容が追加される)。
動作確認
ターミナルを再起動して、例えば `conda list` を実行するとインストールされているパッケージが表示され、きちんとMinicondaがインストールされていることを確認できる。
> conda list # packages in environment at /Users/miniconda3: # # Name Version Build Channel brotlipy 0.7.0 py38h9ed2024_1003 ca-certificates 2020.10.14 0 certifi 2020.6.20 pyhd3eb1b0_3 cffi 1.14.3 py38h2125817_2 chardet 3.0.4 py38hecd8cb5_1003 conda 4.9.2 py38hecd8cb5_0 conda-package-handling 1.7.2 py38h22f3db7_0 cryptography 3.2.1 py38hbcfaee0_1 idna 2.10 py_0 libcxx 10.0.0 1 libedit 3.1.20191231 h1de35cc_1 libffi 3.3 hb1e8313_2 ncurses 6.2 h0a44026_1 openssl 1.1.1h haf1e3a3_0 pip 20.2.4 py38hecd8cb5_0 pycosat 0.6.3 py38h1de35cc_1 pycparser 2.20 py_2 pyopenssl 19.1.0 pyhd3eb1b0_1 pysocks 1.7.1 py38_1 python 3.8.5 h26836e1_1 python.app 2 py38_10 readline 8.0 h1de35cc_0 requests 2.24.0 py_0 ruamel_yaml 0.15.87 py38haf1e3a3_1 setuptools 50.3.1 py38hecd8cb5_1 six 1.15.0 py38hecd8cb5_0 sqlite 3.33.0 hffcf06c_0 tk 8.6.10 hb0a8c7a_0 tqdm 4.51.0 pyhd3eb1b0_0 urllib3 1.25.11 py_0 wheel 0.35.1 pyhd3eb1b0_0 xz 5.2.5 h1de35cc_0 yaml 0.2.5 haf1e3a3_0 zlib 1.2.11 h1de35cc_3
終わりに
インストール後のサイズは300MB強となった。必要なパッケージを入れたらもう少し大きくなるかもしれないが、Anacondaはたしか数GBあったはず。。。
メモ: ベイズ推定 MCMC法のためのPyStanの使い方
はじめに
ベイズ推定で用いるMCMC法の計算をするためのPyStanの使いかたについて簡単な例とともにメモを残す。
問題
平均値既知(10)の標準偏差不明の20個のデータから、標準偏差の値（確率分布）を推定する。
やり方
jupyter notebook使用を想定。
準備
import numpy as np import matplotlib.pyplot as plt import pystan import arviz %matplotlib inline np.random.seed(1)
問題用のデータ生成。平均10、標準偏差0.1としてデータ20個作る。このデータから標準偏差を推定する。
average = 10 sigma = 0.1 data_num = 20 data = np.ones(data_num)*average + np.random.randn(data_num)*sigma
In [ ]: data Out[ ]: array([10.14621079, 9.79398593, 9.96775828, 9.96159456, 10.11337694, 9.89001087, 9.98275718, 9.91221416, 10.00422137, 10.05828152])
PyStanのモデル
データ数N、データY、推定するパラメータ（標準偏差)sigma。モデル（分布の式）は正規分布。PyStanの正規分布はnormal(平均, 標準偏差)と記載。
stan_model = """ data { int N; real Y[N]; } parameters { real<lower=0> sigma; } model { for (n in 1:N){ Y[n] ~ normal(10, sigma); } } """
コンパイル
これでコンパイルが始まる（数十秒〜数分かかる）。上のモデルの記載内容が間違っているとエラーが出るので注意。
sm = pystan.StanModel(model_code=stan_model)
データセット
stan_data = {'N':data.shape[0], 'Y':data}
計算
繰り返し数2000、バーンイン期間(回数)500、同時計算するMCMCの数3。ランダムシードは固定。
fit = sm.sampling(data=stan_data, iter=2000, warmup=500, chains=3, seed=1)
結果
真値0.1に対し、推定値の中心値は0.12。
In [ ]: fit Out [ ]: Inference for Stan model: anon_model_c31d538a0cfaeb031647a7bdeb16c047. 3 chains, each with iter=2000; warmup=500; thin=1; post-warmup draws per chain=1500, total post-warmup draws=4500. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat sigma 0.12 9.3e-4 0.03 0.07 0.09 0.11 0.13 0.19 1198 1.0 lp__ 15.11 0.02 0.73 13.13 14.92 15.39 15.57 15.63 1231 1.0 Samples were drawn using NUTS at Sun Jun 21 11:36:18 2020. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).
arviz.plot_trace(fit)
参考
MCMC法の理屈を知らなくても計算はできるが、理屈は知っておいたほうがよい。以下の図書とオンライン講座が 参考になった。
CNN(Convolutional Neural Network)を用いた画像識別の簡単な例
はじめに
CNNによる画像識別の簡単な例として、下記の波形図の1つ目のピークが高いか2つ目のピークが高いかの識別をPyTorchを使って試みる。
データの準備
画像をCNNで使える配列の形に変換する方法はいくつかあると思うが、ここではpillowを用いた。波形の画像データがフォルダ「testfig」に置いてあるものとして、下記内容でデータを準備した。 （ここでは識別のラベルを、1つ目のピークが高い→0、２つ目のピークが高い→1とし、ファイル名を例えば0-23.pngのように(ラベル)-(画像番号).pngの形式として、ファイル名からラベルを読み込む形としている）
ここで気をつけないといけないのは配列の形状である。PyTorchのCNNの入力の形状[バッチサイズ, チャンネル数, 高さ(ピクセル), 幅(ピクセル)]に合わせないといけない。チャンネル数は画像の奥行き（または深さ）であり、画像の場合は色に対応する。チャンネル数は例えばカラーならR, G, Bの3つ、モノクロなら1つ、などになる。
import glob from PIL import Image import numpy as np # フォルダ testfig においた画像ファイルのリストを取得 image_path = "./testfig" files = glob.glob(image_path + "/*.png") x = [] y = [] for filename in files: # 画像ファイルをndarrayに変換する im = Image.open(filename) im = im.convert("1") # モノクロ画像に変換 im = im.resize((28, 28)) # 28x28にリサイズ im = np.array(im).astype(int) # intのarrayに変換 x.append([im]) # CNNの入力に合うshapeとなるよう注意 # ファイル名から正解ラベルを取得 label = int(filename[len(image_path)+1]) y.append(label) x = np.array(x) # x.shape (画像数, 1, 28, 28) y = np.array(y) # y.shape (画像数,) # 訓練データとテストデータに分ける x_train, x_test, y_train, y_test = \ train_test_split(x, y, test_size=0.2, shuffle=False) # テンソルに変換 x_train = torch.FloatTensor(x_train) y_train = torch.LongTensor(y_train) x_test = torch.FloatTensor(x_test) y_test = torch.LongTensor(y_test) # Dataloaderを準備 train_dataloader = torch.utils.data.TensorDataset(x_train, y_train) train_dataloader = torch.utils.data.DataLoader(train_dataloader, batch_size=4)
ニューラルネットワークの定義
ここでは、畳み込み層→プーリング層→畳み込み層→プーリング層→全結合層→全結合層→出力層という構造とした。最初の全結合層への入力はその直前の層の出力を一次元に変換する必要がある。直前の層の出力サイズの計算は例えばこちら(定番のConvolutional Neural Networkをゼロから理解する - DeepAge)が参考になるが、ここでは高さ・幅が4x4の16チャンネルとなっており、Numpyのviewメソッドを用いて形状の変換を行っている。フィルタ数やフィルタサイズはPyTorchのチュートリアル(Training a Classifier — PyTorch Tutorials 1.4.0 documentation)を参考に適当に決めた。
from sklearn.model_selection import train_test_split import torch import torch.nn as nn import torch.nn.functional as F class Model(nn.Module): def __init__(self): super(Model, self).__init__() self.conv1 = nn.Conv2d(1, 6, 5) # チャンネル1, フィルタ6, フィルタサイズ5x5 self.pool1 = nn.MaxPool2d(2, 2) # 2x2のプーリング層 self.conv2 = nn.Conv2d(6, 16, 5) # チャンネル6, フィルタ16, フィルタサイズ5x5 self.pool2 = nn.MaxPool2d(2, 2) # これまでの畳込みとプーリングで、16チャンネルの4x4が入力サイズ self.fc1 = nn.Linear(16 * 4 * 4, 64) # fc: fully connected self.fc2 = nn.Linear(64, 16) self.fc3 = nn.Linear(16, 2) def forward(self, x): x = F.relu(self.conv1(x)) x = self.pool1(x) x = F.relu(self.conv2(x)) x = self.pool2(x) x = x.view(-1, 16 * 4 * 4) # [(バッチサイズ), (一次元配列データ)]に並び替え x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) x = self.fc3(x) return x
学習
Dataloaderを使ってミニバッチ学習させた。学習に関してはCNNだからといって特別なところはない。
model = Model() criterion = nn.CrossEntropyLoss() optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9) num_epochs = 20 for epoch in range(num_epochs): total_loss = 0.0 for inputs, labels in train_dataloader: optimizer.zero_grad() outputs = model(inputs) loss = criterion(outputs, labels) loss.backward() optimizer.step() total_loss += loss.item() print('Epoch: {} Loss: {}'.format(epoch, total_loss))
検証(正答率の確認)
はじめに準備したテストデータを用いて正答率を確認。
outputs = model(x_test) _, predicted = torch.max(outputs.data, 1) correct = (y_test == predicted).sum().item() # Tensorの比較で正答数を確認 print("正答率: {} %".format(correct/len(predicted)*100.0))
結果
問題が単純なためか、正答率は高い。
Epoch: 0 Loss: 6.9794119000434875 Epoch: 1 Loss: 6.852706849575043 Epoch: 2 Loss: 6.788195848464966 Epoch: 3 Loss: 6.761787533760071 Epoch: 4 Loss: 6.738182067871094 Epoch: 5 Loss: 6.654882311820984 Epoch: 6 Loss: 6.485922873020172 Epoch: 7 Loss: 6.05694118142128 Epoch: 8 Loss: 5.022340148687363 Epoch: 9 Loss: 2.5453680232167244 Epoch: 10 Loss: 0.31626373156905174 Epoch: 11 Loss: 0.011260125378612429 Epoch: 12 Loss: 0.0037041376635897905 Epoch: 13 Loss: 0.00182408066757489 Epoch: 14 Loss: 0.0011753853141271975 Epoch: 15 Loss: 0.0009152144466497703 Epoch: 16 Loss: 0.0007907451872597449 Epoch: 17 Loss: 0.0007194795762188733 Epoch: 18 Loss: 0.0006725111852574628 Epoch: 19 Loss: 0.0006386453569575679 正答率: 100.0 %
参考
・シンプルな CNN | PyTorch で簡単なニューラルネットワークを構築し画像を分類する方法
シンプルな例で詳しく説明されています。
・Pytorchのニューラルネットワーク(CNN)のチュートリアル1.3.1の解説 - Qiita
畳み込みの部分が図を用いて詳しく説明されています。
・CNN（Convolutional Neural Network）を理解する - sagantaf
フィルタサイズやパディング、ストライドの影響について解説があります。
・Convolutional Neural Networkとは何なのか - Qiita
CNNが具体的に何を見ているかについてわかりやすい説明があります。
Chainer 開発終了
Chainerが開発終了の模様です。
こういうことがあるのでフレームワークや言語選びは悩みますね。 はじめはChainerを使おうとしていたのですが、PyTorchにしておいてひとまず良かったようです。
メモ: Pillowを用いた深層学習用の画像データ数値化
画像データの深層学習を行うためのPillowを用いた画像データ数値化のメモ。 次の適当な画像データを、深層学習に使えるように数値化する。
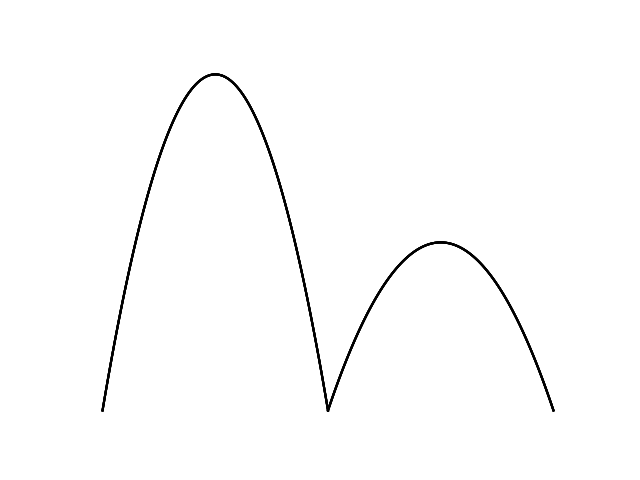(testfig.png)
from PIL import Image import numpy as np im = Image.open("./testfig.png") # 画像ファイル読み込み im = im.convert("L") # 画像のモード変更 "L"は8bitグレイスケール im = im.resize((256, 256)) # 画像サイズ変更 data = np.array(im) # 画像を配列として数値データ化 im.show() # 処理後の画像表示
カラー、透過度等も含めたその他の画像モードは下記リンク参考
Concepts — Pillow (PIL Fork) 6.2.1 documentation
その他参考
